比尔-朗伯定律
比尔-朗伯定律(Beer–Lambert law),又称比尔定律或比耳定律(Beer's law)、朗伯-比尔定律、布格-朗伯-比尔定律(Bouguer–Lambert–Beer law),是光吸收的基本定律,适用于所有的电磁辐射和所有的吸光物质,包括气体、固体、液体、分子、原子和离子。比尔-朗伯定律是吸光光度法、比色分析法和光电比色法的定量基础。
比尔-朗伯定律(Beer–Lambert law),又称比尔定律或比耳定律(Beer's law)、朗伯-比尔定律、布格-朗伯-比尔定律(Bouguer–Lambert–Beer law),是光吸收的基本定律,适用于所有的电磁辐射和所有的吸光物质,包括气体、固体、液体、分子、原子和离子。比尔-朗伯定律是吸光光度法、比色分析法和光电比色法的定量基础。
概述
一束单色光照射于一吸收介质表面,在通过一定厚度的介质后,由于介质吸收了一部分光能,透射光的强度就要减弱。吸收介质的浓度愈大、介质的厚度愈大,则光强度的减弱愈显著,其关系为:
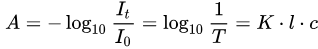
其中:
-
:吸光度;
-
:入射光的强度;
-
:透射光的强度;
-
:透射比,或称透光度;
-
:系数,可以是吸收系数或摩尔吸收系数,见下文;
-
:吸收介质的厚度,一般以 cm 为单位;
-
:吸光物质的浓度,单位可以是 g/L 或 mol/L。
比尔-朗伯定律的物理意义是,当一束平行单色光垂直通过某一均匀非散射的吸光物质时,其吸光度 


当介质中含有多种吸光组分时,只要各组分间不存在着相互作用,则在某一波长下介质的总吸光度是各组分在该波长下吸光度的加和,这一规律称为吸光度的加合性。
系数 
- 当介质厚度
以 cm 为单位,吸光物质浓度
以 g/L 为单位时,
用
表示,称为吸收系数,其单位为 L⋅g−1⋅cm−1
。这时比尔-朗伯定律表示为
。
- 当介质厚度
以 cm 为单位,吸光物质浓度
以 mol/L 为单位时,
用
表示,称为摩尔吸收系数,其单位为 L⋅mol−1⋅cm−1
。这时比尔-朗伯定律表示为
。
两种吸收系数之间的关系为:
历史
物质对光吸收的定量关系很早就受到了科学家的注意并进行了研究。皮埃尔·布格(Pierre Bouguer)和约翰·海因里希·朗伯(Johann Heinrich Lambert)分别在1729年和1760年阐明了物质对光的吸收程度和吸收介质厚度之间的关系;1852年奥古斯特·比尔(August Beer)又提出光的吸收程度和吸光物质浓度也具有类似关系,两者结合起来就得到有关光吸收的基本定律布格-朗伯-比尔定律,简称比尔-朗伯定律。












