OSA-UCS

在比色法中，OSA-UCS（美国光学学会统一色标）是一种色彩空间，于 1947 年首次发布，由美国光学学会统一色标委员会开发。以前创建的色序系统（例如 Munsell 颜色系统）无法表示所有方向的感知均匀性。委员会决定，为了准确表示每个方向上的均匀色差，需要使用三维笛卡尔几何的新形状。

历史和发展

OSA-UCS 的开发历经 1947 年至 1977 年多年。在 CIE 开发第一个数学颜色模型后不久，David MacAdam 表明，在 CIE 色度图上选择颜色时，无法保证围绕该颜色的相同感知色差的颜色相对于参考颜色处于相同的颜色距离。更简单地说，色度图上任意两种颜色之间的欧几里得距离不能用作感知色差的统一度量。在这一发现之后，人们立即开始创造一个在色差的所有方向上表现一致的空间。

从 59 个色差不均匀的彩色瓦片样本开始，OSA 要求 72 名观察者判断不同样本瓦片之间的色差。根据收集的数据，开发了公式并定义了参数以创建新的统一色彩空间。他们选择了参考 10 度观察器和光源 D65 来表征均匀空间和 30% 反射率的中性灰色背景。最后，制作了 558 个颜色样品 - 424 个全步和 54 个半步 - 并由 OSA 分发。

几何

立方八面体

点与中心点的距离相等的理想彩色纯色是球体 - 但是，球体的集合不能被压缩以形成一个更大的实体而没有间隙。OSA 最终选择的几何结构是基于立方八面体的菱面体晶格。此实体的 12 个顶点中的每一个与中心以及每个相邻顶点的距离相等。完成此几何图形的最后一步是重新缩放垂直 L 轴，以实现颜色描述的整数坐标位置。颜色距离均匀性保持不变，因为仅缩放轴尺寸，并且缩放在颜色距离公式中考虑。

坐标值

OSA-UCS 的三个垂直维度是亮度维度 L、黄化维度 j（黄色/蓝色对手维度）和绿色维度 g（绿色/红色对手维度）。

亮度 （L）

OSA-UCS 纯色的亮度等级在垂直方向上变化，范围约为 -10 到 8。UCS 亮度为 0 对应于为其样本选择的 30% 反射中性背景灰色，而较亮的阴影具有正值，较暗的阴影具有负值。

Jaune （j）

OSA-UCS 纯色的黄化维度水平延伸并垂直于 L 维度。这是一个黄蓝色色度维度，从正值显示更淡黄色到负值显示更蓝。j 值为 0 时，沿中性轴表示。

绿色 （g）

OSA-UCS 的绿色尺寸垂直于 L 和 j 尺寸水平延伸。此绿-红色轴从更偏绿的正值到更偏粉的负值不等。同样，g 值 0 位于中性 （L） 轴上。

颜色分组

OSA-UCS 彩色实体的立方八面体结构在几何上可以分为 9 个平面，称为解理面。这 9 个解理面定义为：

L - 垂直于 L 轴的常数 L（亮度）平面，其中 j 和 g 可以采用任何值。

j - 垂直于 j 轴的常数 j（黄蓝）平面，其中 L 和 g 可以采用任何值。

g - 垂直于 g 轴的常数 g（红绿）平面，其中 L 和 j 可以采用任何值。

L+j - 平行于 g 轴的常数 L+j 平面，与 L 轴成 35°，与 j 轴成 55°。

L-j - 与 g 轴平行的常数 L-j 平面，与 L 轴成 35°，与 j 轴成 55°。

L+g - 平行于 j 轴、与 L 轴成 35° 与与 g 轴成 55° 的常数 L+g 平面。

L-g - 与 g 轴平行的常数 L-g 平面，与 L 轴成 35°，与 g 轴成 55°。

j+g - 与 L 轴平行，与 j 轴和 g 轴成 45° 的常数 j+g 平面。

j−g - 一个常数 j-g 的平面，平行于 L 轴，与 j 轴和 g 轴成 45° 角。

色差

OSA-UCS 色差由色彩空间中两种颜色之间的简单欧几里得距离定义，该距离考虑了对 L 轴所做的缩放。用于计算颜色 1 和 2 之间色差的公式是：

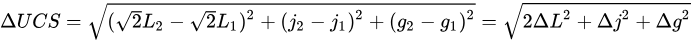
由于系统的设计，OSA-UCS 颜色空间中两个相邻域之间的色差始终为 2。使用此公式可以准确计算出微小的色差。但是，较大的色差需要非线性校正才能获得准确性。