全反射

光学描述

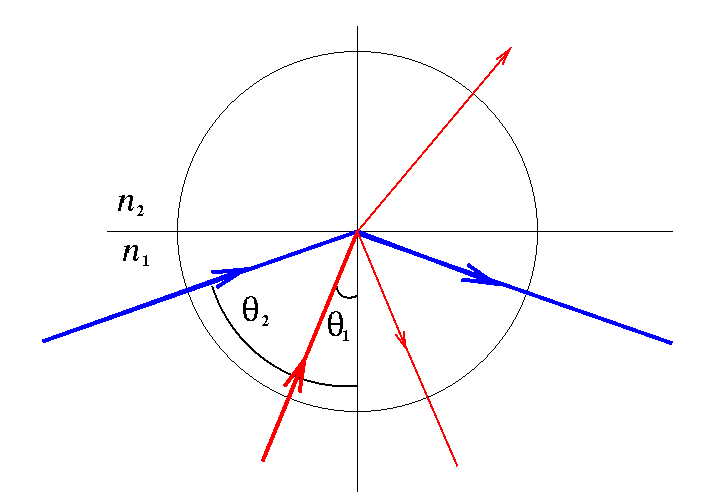
如图一所示： 光线从折射率较高的  n 1 {\displaystyle n_{1}}  介质进入折射率较低的  n 2 {\displaystyle n_{2}}  介质： 当入射角  θ i = θ 1 {\displaystyle \theta _{i}=\theta _{1}}  即少于临界角  θ c {\displaystyle \theta _{c}}  时，光线同时发生趋离  n 2 {\displaystyle n_{2}}  介质(normal)的折射，以及向  n 1 {\displaystyle n_{1}}  介质的反射（图一中红色光线所示）； 当入射角  θ i = θ 2 {\displaystyle \theta _{i}=\theta _{2}}  即大于临界角  θ c {\displaystyle \theta _{c}} 时，  n 2 {\displaystyle n_{2}}  介折射的光线消失，所有光线向  n 1 {\displaystyle n_{1}}  介质中(英语：normal)反射（图一中蓝色光线所示）； 全内反射仅仅可能发生在当光线从较高折射率的介质（也称为光密介质）进入到较低折射率的介质（也称为光疏介质）的情况下，例如当光线从玻璃进入空气时会发生，但当光线从空气进入玻璃则不会。

 O 1 × sin ⁡ α g r = O 2 × sin ⁡ β {\displaystyle O_{1}\times \sin \alpha _{gr}=O_{2}\times \sin \beta } 

例如：

•  O 1 {\displaystyle O_{1}} 为光纤核心折射率 (英语：refractive index)  ≈ {\displaystyle \approx }  1.5
•  O 2 {\displaystyle O_{2}}  为空气折射率 (英语：refractive index) = 1
•  β {\displaystyle \beta }  =  90 ∘ {\displaystyle 90^{\circ }} 
•  α g r {\displaystyle \alpha _{gr}} =未知

 arcsin {\displaystyle {\displaystyle \arcsin }}  ( ( 1 × sin ⁡ 90 ∘ ) / 1.5 ) = α g r {\displaystyle ((1\times \sin 90^{\circ })/1.5)=\alpha _{gr}} 

那么空气和光纤核心临界角(  θ c {\displaystyle \theta _{c}} )为  α g r {\displaystyle \alpha _{gr}} 

临界角

临界角（英语：Critical angle）是使得全内反射发生的最少的入射角。入射角是从折射界面的法线量度计算的。临界角（ θ c {\displaystyle \theta _{c}} ）可从以下方程计算：

 θ c = arcsin ⁡ n 2 n 1 {\displaystyle \theta _{c}=\arcsin {\frac {n_{2}}{n_{1}}}} 

其中 n 2 {\displaystyle \!n_{2}} 是较低密度介质的折射率，及 n 1 {\displaystyle \!n_{1}} 是较高密度介质的折射率。这条方程是一条斯涅尔定律的简单应用，当中折射角为90°。 当入射光线是准确地等于临界角，折射光线会循折射界面的切线进行。以可见光由玻璃进入空气（或真空）为例，临界角约为48.7°。